The ability to control complex convective flow patterns is important in both technology and fundamental science. In many technological processes, the naturally occurring flow patterns may not be the optimal ones. By controlling the flow, one may be able to optimize the process, improve product quality, and achieve significant savings. The ability to stabilize otherwise non-stable states may also assist one in gaining deeper insights into the dynamics of flows. Since fluid flow phenomena are highly nonlinear and possess many degrees of freedom, the flow control problem is far from trivial. Nevertheless, significant progress has been made in recent years.
Our Projects:
Thermal Convection Loops
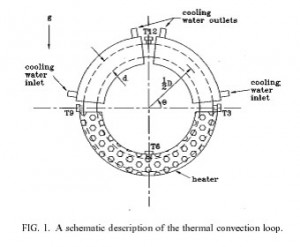
The thermal convection loop consists of a liquid filled torus standing in the vertical plane. The lower half of the torus is heated and the upper half of the torus is cooled. The thermal convection loop is a relatively simple experimental paradigm that exhibits complex dynamic behavior. As the heating rate increases, the flow in the loop undergoes a sequence of bifurcations from a motionless state to time-independent convection to chaotic flow. The loop provides a convenient platform for studying chaotic dynamics and evaluating and comparing various control strategies. In prior experimental and theoretical investigations, Singer, Wang & Bau (1991), Singer & Bau (1991), Wang, Singer & Bau (1992), Yuen & Bau (1996), Yuen (1997), and Yuen and Bau (1998) used various linear and nonlinear control strategies to alter the bifurcation structure of the convective motion in a thermal convection loop. For example, with the aid of a controller, they were able to delay the transition from a no-motion to a motion state, laminarize the naturally occurring chaotic motion in the loop, stabilize otherwise non-stable periodic orbits embedded in the chaotic attractor, render subcritical bifurcations supercritical, and induce chaos under conditions in which the flow normally would be laminar.
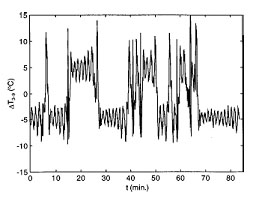
FIG. 2: The experimentally observed temperature difference between positions 3 and 9 o’clock is depicted as a function of time. The Rayleigh number is three times the critical Rayleigh number when chaos is first observed.
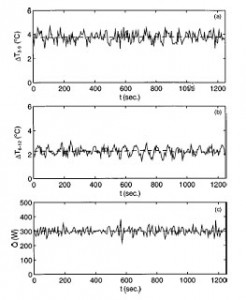
FIG. 3: Experimental observations of the flow in the controlled thermal convection loop. The conditions are similar to the ones in Fig. 2. The temperature difference between positions 3 and 9 o’clock (a), the temperature difference between positions 6 and 12 o’clock (b), and the power fluctuations (c) are depicted as functions of time. Witness that the controller requires relatively small power modulations.
PUBLICATIONS
- Bau, H. H., 1991, On Controlling a Chaotic System, Modern Physics Letters B, 5, 1489-1497.
- Singer J., & Bau, H. H., 1991, Active Control of Convection, Physics of Fluids A, 3 (12), 2859-2865.
- Wang Y-Z, & Bau, H. H., 1992, Thermal Convection Loop with Heating from Above, Int. J. Heat and Mass Transfer, 35, 111-120.
- Wang Y., Singer J., and Bau, H. H., 1992, Controlling Chaos in a Thermal Convection Loop, J. Fluid Mechanics, 237, 479-498.
- Yuen, P. K., & Bau, H. H., Rendering Subcritical Hopf Bifurcation Supercritical, J. Fluid Mechanics, 317, 91-109, 1996.
- Yuen, P. K., & Bau, H. H., Controlling Chaotic Convection Using Neural Nets – Theory and Experiments, Neural Networks, 11, 557 – 569, 1998.
- Yuen, P., K., & Bau, H. H., 1999, Optimal and Adaptive Control of Chaotic Convection – Theory and Experiments, Physics of Fluids, 11, Issue 6, 1435-1448.
Rayleigh-Benard
We are investigating the feasibility of delaying the transition from the no-motion (pure conduction) to the motion state in the Rayleigh-Benard (RB) problem of a fluid layer heated from below and cooled from above. We have chosen this problem for study because the uncontrolled problem has been extensively studied and the phenomena observed are relatively well understood. The RB problem is also of technological importance since it serves as a paradigm for many material processing applications.
In theoretical studies, Tang & Bau (1993a, b, 1994, 1995, and 1998) have shown that with the aid of a feedback controller the critical Rayleigh number for the onset of convection in an infinite horizontal fluid layer can be increased by almost an order of magnitude. Our experiments demonstrated (Tang & Bau, 1998) a more modest success. Currently, we are improving the experiments to bridge the gap between theoretical predictions and experimental observations, investigating the limitations of linear control strategies, and devising non-linear controllers.
FIG. 1: The normalized critical Rayleigh (R/1707) and wave (a/3.117) numbers are depicted as functions of the thermal controller’s gain (Kp). The solid and dotted curves describe, respectively, loss of stability through a real eigenvalue (exchange of stability) and through a Hopf bifurcation.
PUBLICATIONS
- Tang, J., & Bau, H. H., 1993, Stabilization of the No-motion State in Rayleigh-Bénard Convection Through the Use of Feedback Control, Physical Review Letters, 70, 1795-1798.
- Tang, J., & Bau, H. H., 1993, Feedback Control Stabilization of the No-motion State of a Fluid Confined in a Horizontal, Porous Layer Heated from Below, J. Fluid Mechanics, 257, 485-505.
- Bau, H., H., 1993, Controlling Chaotic Convection, (an invited paper) in Theoretical and Applied Mechanics 1992, (Proceedings of the XVIIIth International Congress of Theoretical and Applied Mechanics, Haifa, Israel, August 22-28), S. R. Bonder, J. Singer, A. Solan, and Z. Hashin, editors, Elsevier Science Publishers, 187-203.
- Tang, J., and Bau, H. H., 1994, Stabilization of the No-motion State in the Rayleigh-Bénard Problem, Proceedings Royal Society A, 447, 587-607.
- Tang, J., and Bau, H. H., 1995, Stabilization of the No-motion State of a Horizontal Fluid Layer Heated from Below with Joule Heating, Trans. ASME-J. Heat Transfer, 117, 329-333.
- Tang, J., & Bau, H. H., Experiments on the Stabilization of the No-Motion State of a Fluid Layer Heated From Below and Cooled from Above, J. Fluid Mechanics, 363, 153-171, 1998.
- Tang, J., & Bau, H. H., 1998, Numerical Investigation of the Stabilization of the No-Motion State of a Fluid Layer Heated from Below and Cooled from Above, Physics of Fluids, 10, Issue 7, 1597-1610
- Zhao, H., and Bau, H., H., 2006, On the Limitations of Linear Control of Thermal Convection in a Porous Medium (PF#06-0204A), Physics of Fluids, 18, 074109, 1-12.
- Remillieux, M., Zhao, H., and Bau, H. H., 2007, Suppression of Rayleigh-Benard Convection with Proportional-Derivative (PD) Controller, Physics of Fluids 19, 017102
Marongoni-Benard Convection
PUBLICATIONS
Bau, H., H., 1999, Control of Marangoni-Benard Convection, Int. J. Heat Mass Transfer, 42, 1327-1341.